GeoGebra必学必用经验
Author : zbzhen, Modified : Fri Jan 2 20:17:16 2026
本文来源 https://kz16.top/ggb/ggbpptReadMe.html
-
GeoGebra(官网 https://geogebra.org/ , 音译: 几何不难)是一款开源跨平台的非商用免费软件, 一定要注意商用无价, 当心被坑. GeoGebra有三个版本, 分别是版本5, 版本6和网页版, 点我查看三者的区别. -
ggb多页模板(官网 https://kz16.top/ggb) 基于GeoGebra网页版开发, 免费开源, 双向兼容ggb, 提供多页面功能, 也提供实用模板, 并支持插入到PPT
-
ggb多页模板3.4备用下载地址:https://kz16.lanzouu.com/iJNux3d55tij 密码:6666 一定要解压后使用 -
注意: 3.4版本集成了多功能: 插入PPT(兼容苹果), 多页面功能, ggb编辑器(左上角ggb按钮可打开), js编辑器.
-
官方Q群: 928916608 (ggb多页模板官方群)
-
推荐搭配软件: 谷歌浏览器, 谷歌浏览器win7旧版, 讯飞输入法
数学绘图是一种可以复制的艺术
数学功底决定绘图造诣
1. ggb多页模板教程
1.1. ggb多页模板简介
GeoGebra是一款可用于制作动态交互演示的软件, 尽管已经写入人教教科书, 它依旧存在诸多缺陷: 默认样式丑, 无法动态插入到ppt, 没有多页功能, 打开速度巨慢, 不方便直接演示...
ggb多页模板基于GeoGebra网页版开发, 并且完全双向兼容官方课件, 它的优势有:
-
良心公益: 永久免费开源, 体积小, 免安装, 可U盘携带, 跨平台(支持windows/mac/linux), 无广告, 无隐私获取, 无注册登录扫描关注等套路
-
多页便捷: 支持一次性复制粘贴导入多个ggb文件; 页面命名, 交换页面位置, 克隆与删除页面; 激光笔翻页
-
模板精美: 常用的点, 线条以及标签大小和样式美观; 坐标系和箭头好看, 并且函数会自适应坐标系范围, 彻底杜绝图文打架现象; 此外一键导出的svg矢量图和绘制过程中的图样式一致, 并且放大缩小不失真.
-
按钮实用: 通过拖动左上角滑条, 可彻底解决分辨率问题, 以及界面大小调整的问题; 其它一些实用按钮, 例如, 一键svg矢量图导出, 一键导出所有页面, 一键清爽预览页面, 一键导入或导出base64代码, 一键中英文切换, 一键查看详细教程, 一键保存和分享
-
演示方便: 全屏播放, 翻页, 笔迹, 时间显示等按钮已经可用于日常教学演示; 不用担心分辨率问题; 演示清晰度比桌面版要好很多;
-
可插入ppt: 可以轻松把多个ggb文件转变为ppt文件
-
ggb代码编辑器: 借助Qwen模型, 实现完全离线的ggb代码提示和补全功能
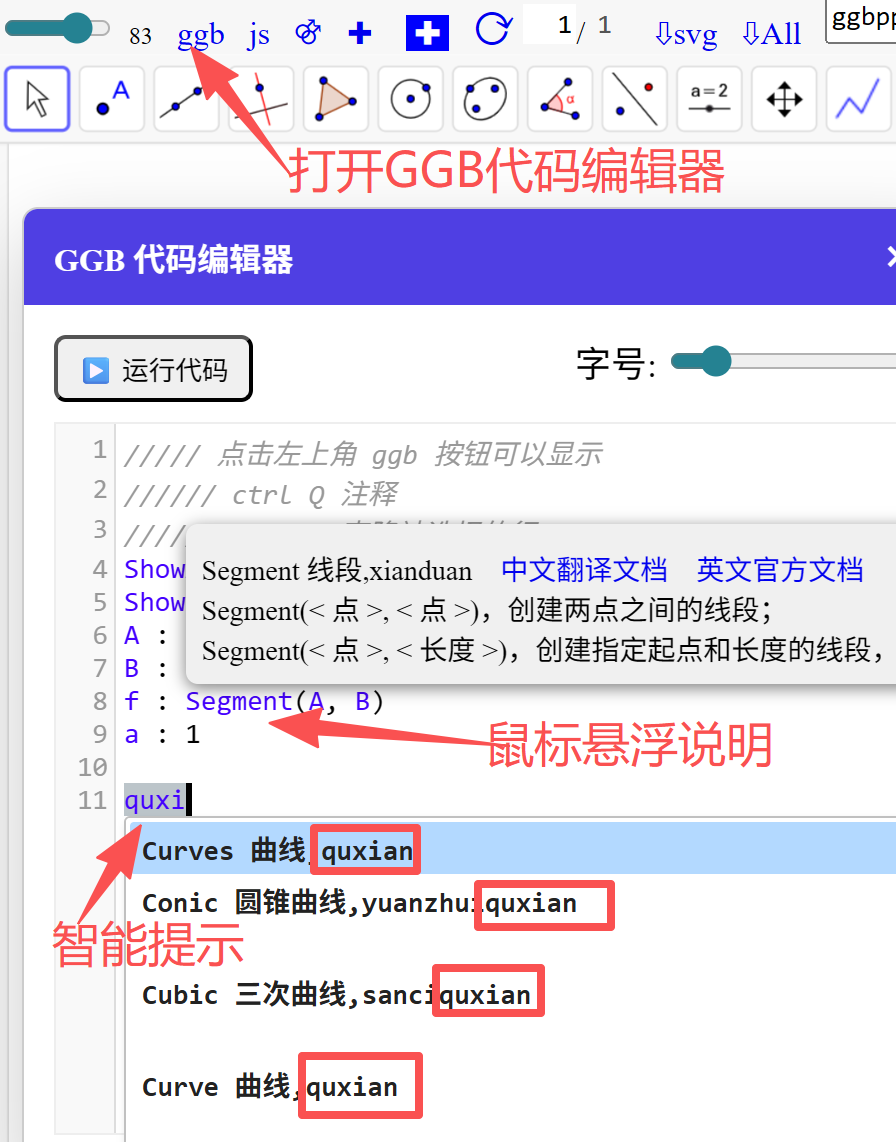
1.2. 交互课件插入到ppt中
苹果电脑和linux系统稍微复杂, 具体参考教程 苹果电脑怎么把ggb插入到ppt中
1.2.1. 准备工作
-
安装wps
-
下载并解压
ggb多页模板3.4版离线包ggbv3.4 -
最新版本已经无需安装
ggb桌面程序与催化剂插件
1.2.2. 操作步骤
旧版本步骤繁琐, 新版本只需要简单两步: 启动 + 一键导出ppt
-
进入
ggb多页模板文件夹, 打开启动.bat, 会自动打开预览界面
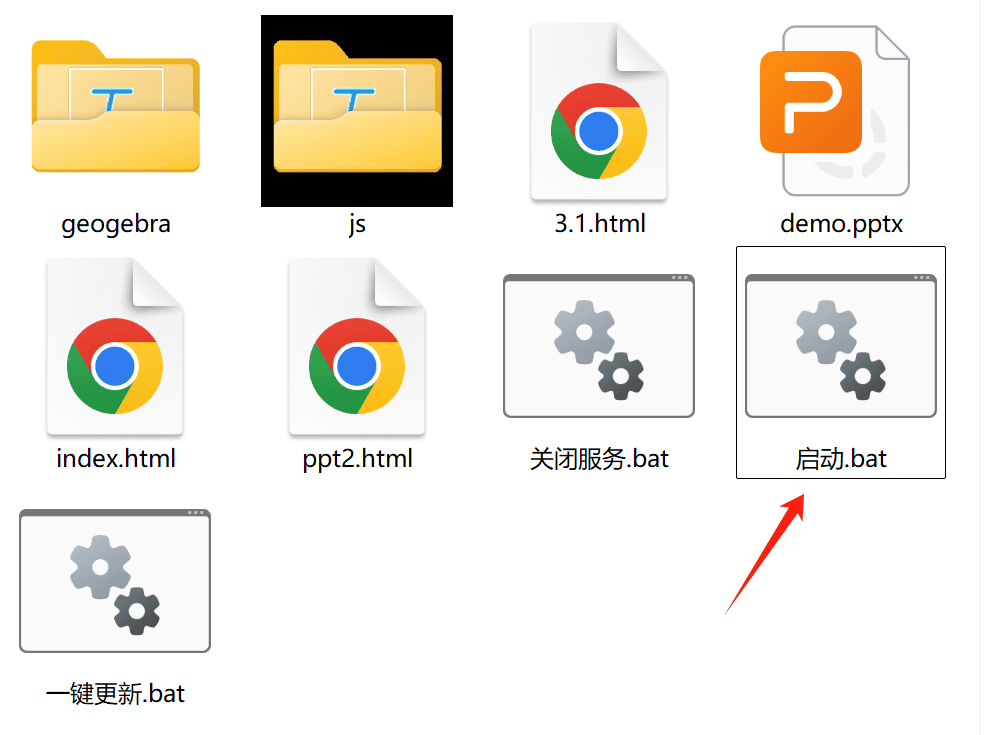
-
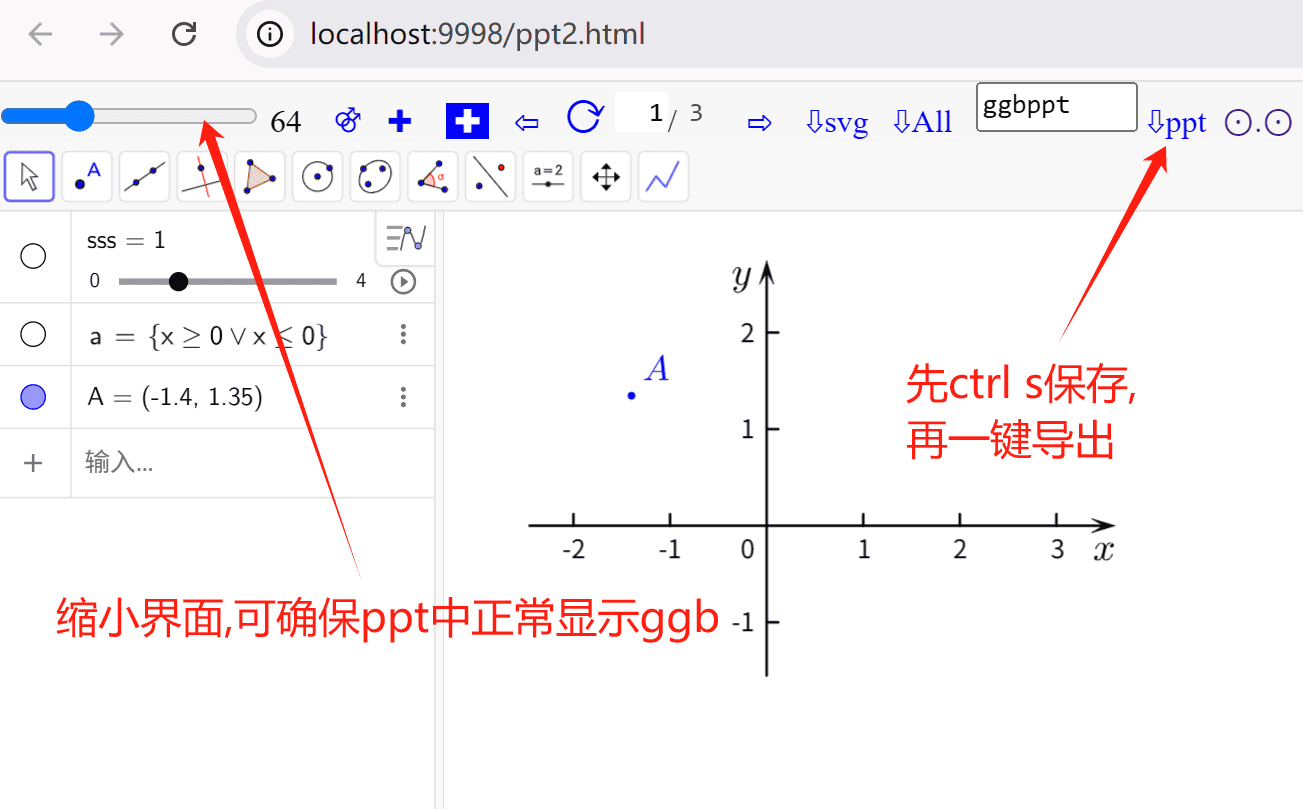
在预览页面里点击
编辑进入编辑界面, 绘制数学物理交互动图, 然后要记得ctrl s保存, 最后点击⇩PPT按钮一键导出ppt.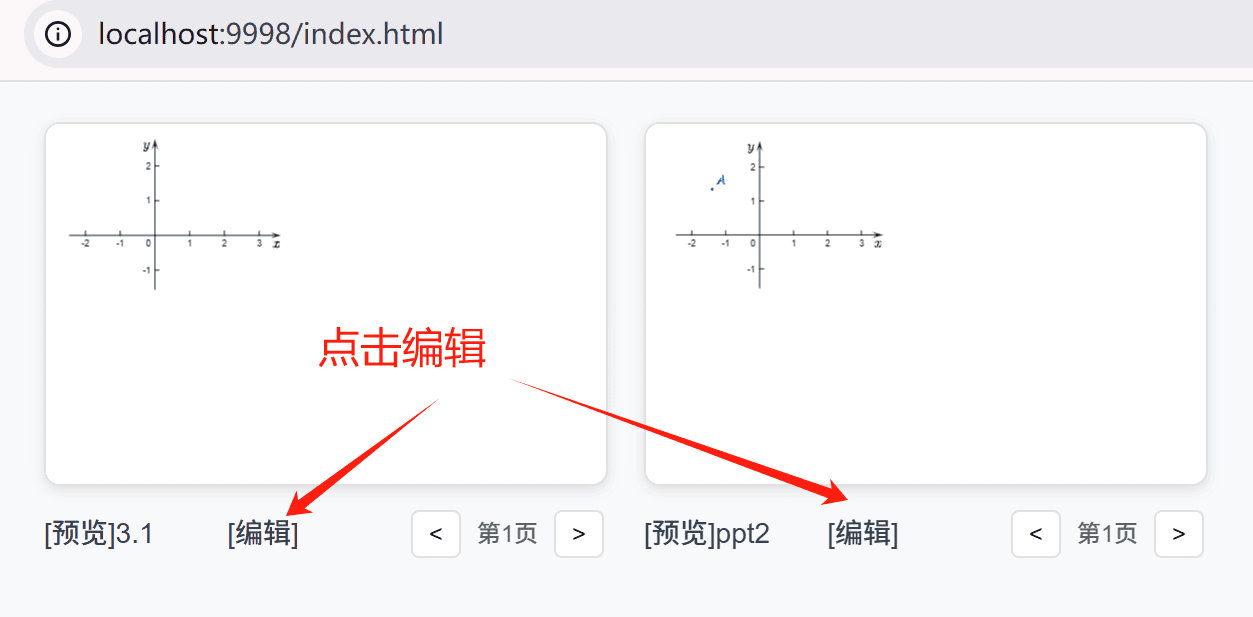
1.2.3. 多个ggb怎么转变为ppt?
和前面的操作步骤一样, 只是多一步把ggb复制粘贴到编辑界面
-
打开
启动.bat并进入编辑界面 -
先ctrl c复制多个ggb文件, 再ctrl v粘贴到编辑界面, 然后要记得ctrl s保存, 最后点击
⇩PPT按钮一键导出ppt.
1.2.4. ppt中编辑ggb并保存
在ppt中编辑ggb动图, 无法用快捷键 ctrl S保存,
但是可以点击ggb图后, 然后用组合快捷键 ctrl Shift 字母o 保存
1.3. 做好的ppt在新电脑上演示
假设已经成功在电脑上把ggb插入到ppt里, 想让好友也能演示, 或者在教室里可演示, 只需两步
-
把自己电脑里的
ggbv3.4文件夹复制到教室电脑 -
打开
ggbv3.4中的启动.bat
1.4. ggb多页模板插入到markdown笔记软件中
要插入到markdown笔记软件中, 则直接用下面的格式
<iframe src="http://localhost:9998/3.4.html?page=1&zoom=0.6" width="500" height="500" frameborder="0"></iframe>
该链接可以通过预览⊙.⊙按钮得到方式, page=1表示第一个页面,zoom=0.6 表示缩放.
自己部署的方案, 例如
<iframe src="https://kz16.top/ggb/index.html?page=1&zoom=0.6&w=300&h=400" width="400" height="200" frameborder="0"></iframe> <iframe src="https://kz16.top/ggb/index.html?page=1&zoom=0.6" width="400" height="200" frameborder="0"></iframe>
其中&w=300&h=400 分别可以调整高度和宽度
1.5. ggb官方链接插入到markdown笔记软件中
当然还可以使用官方的链接, 例如
// 二维图 <iframe src="https://www.geogebra.org/material/iframe/id/fph9pf2x/width/400/height/400/" width="400px" height="400px" style="border:0px;"> </iframe> // 三维图需要加上 sdz/true, 确保三维图可以调整视角 <iframe src="https://www.geogebra.org/material/iframe/id/c5s3gwmz/width/400/height/400/sdz/true" width="400px" height="400px" style="border:0px;"> </iframe>
具体参考官方说明文档: https://wiki.geogebra.org/en/Reference:Material_Embedding_(Iframe)
问题: 官网https链接怎么生成?
回答 在 https://kz16.top/ggb/ 登陆官方账号, 然后依次点右上角按钮三-->share(分享)就可以得到官网链接
1.6. ggb多页模板基本功能说明
1.6.1. 主要按钮说明
ggb多页模板相比GeoGebra网页版或者经典6, 大体上没什么区别, 只是多了一些实用按钮
按钮分为三个区域: 顶部, 底部, 目录
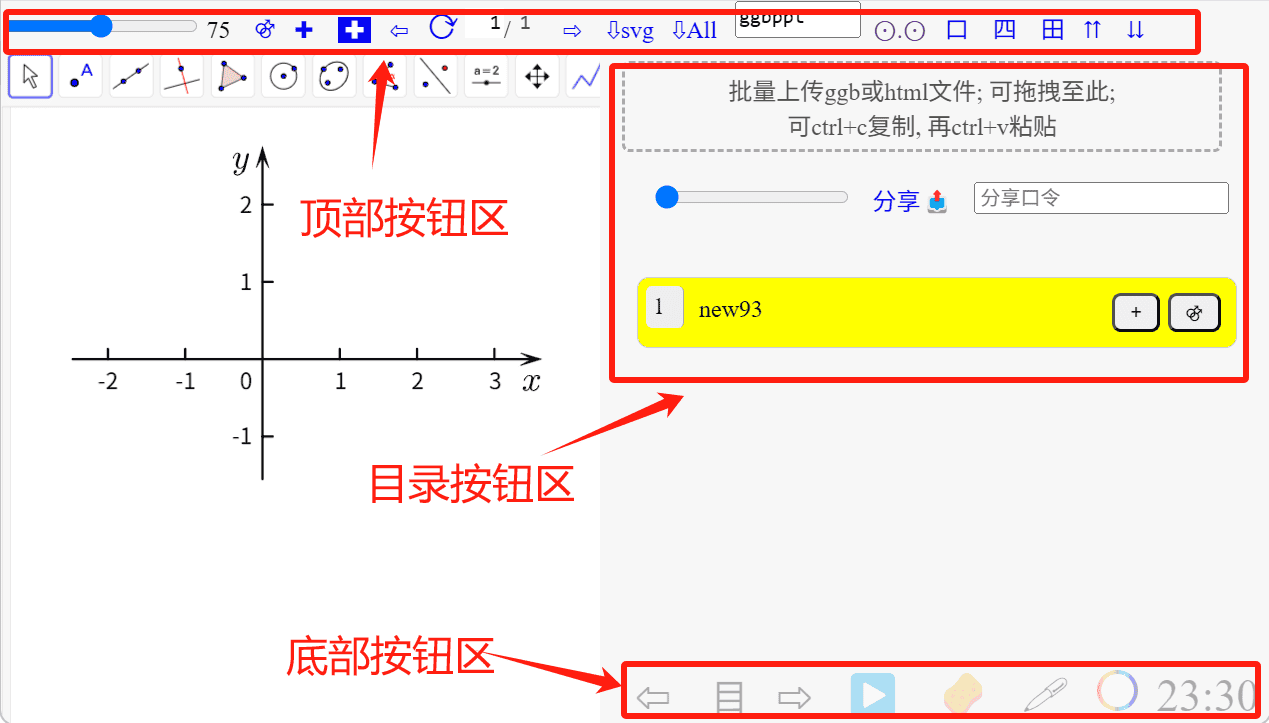
-
▶️显示或隐藏顶部按钮区域, 并且会全屏展示 -
目显示或隐藏目录区域 -
⟳显示或隐藏底部区域按钮
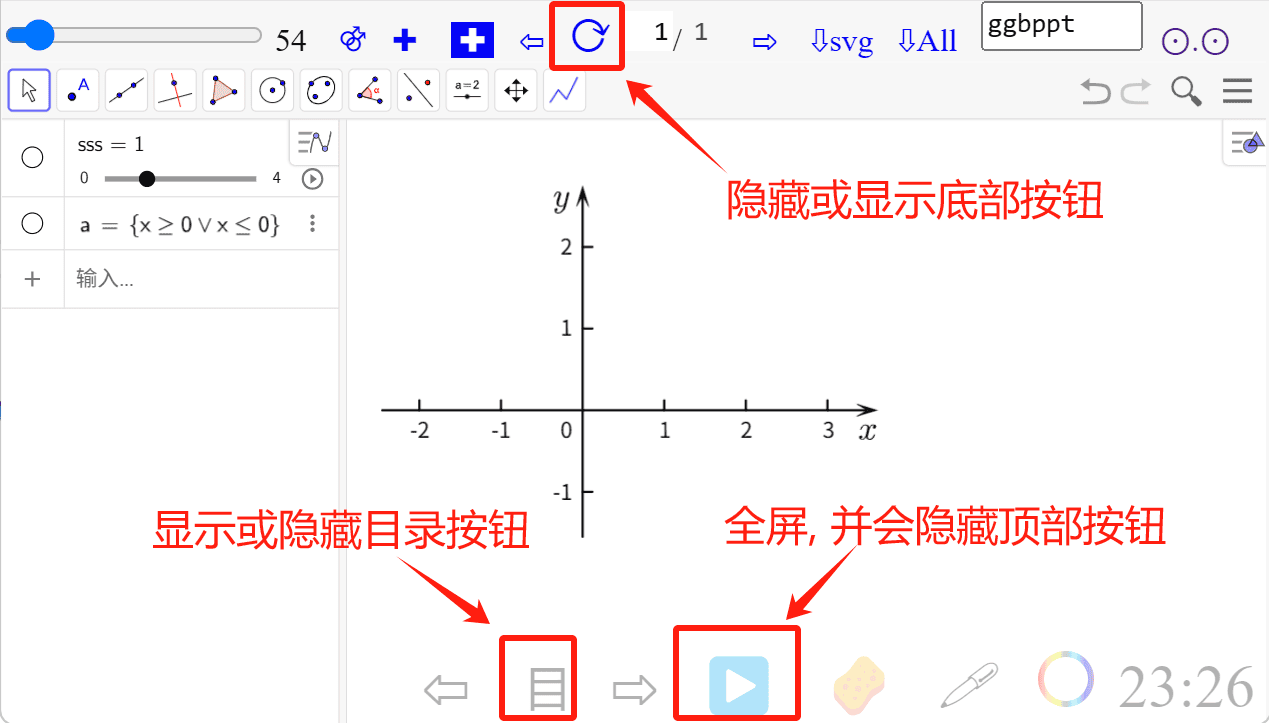
1.6.2. 多页操作
点击底部 目 可以显示目录区域, 鼠标拖拽目录的边缘可调整目录区域的范围
-
X删除页面 -
↶恢复删除的页面 -
✚新加页面 -
⚣克隆页面 -
点击页面名字可以直接修改名称
-
将一个页面拖拽到另外一个页面上可以交换页面顺序
-
键盘↑ ↓方向键或者鼠标点击⇦⇨按钮或者拖动页面进度条或者点击目录序号可翻页
1.6.3. 几何模板与函数模板
✚按钮为几何模板, 用于绘制几何图,- ✚ 按钮为函数模板, 包含了精美的坐标系
1.6.4. 播放与笔迹
演示按钮都在右下角
-
彩环按钮勾选后, 可绘制能自动消失的多彩笔迹 -
🖊笔按钮, 两次点击后可进入ggb绘图模式, 同时保留笔迹 -
🧽橡皮擦按钮, 被点击后, 会出现框选擦除, 以及清屏选项; 点击清屏会自动下载透明笔迹图片, 并且清除笔迹 -
▶️播放按钮不仅可用于全屏展示, 3次点击后, 可清除页面笔迹
1.6.5. 导入ggb与html多页文件
-
支持一次性导入多个ggb与html多页文件
- 方法一: crtl c复制多个ggb与html多页文件, 再crtl v粘贴即可
- 方法二: 点击
目按钮打开目录区域, 会有详细说明
-
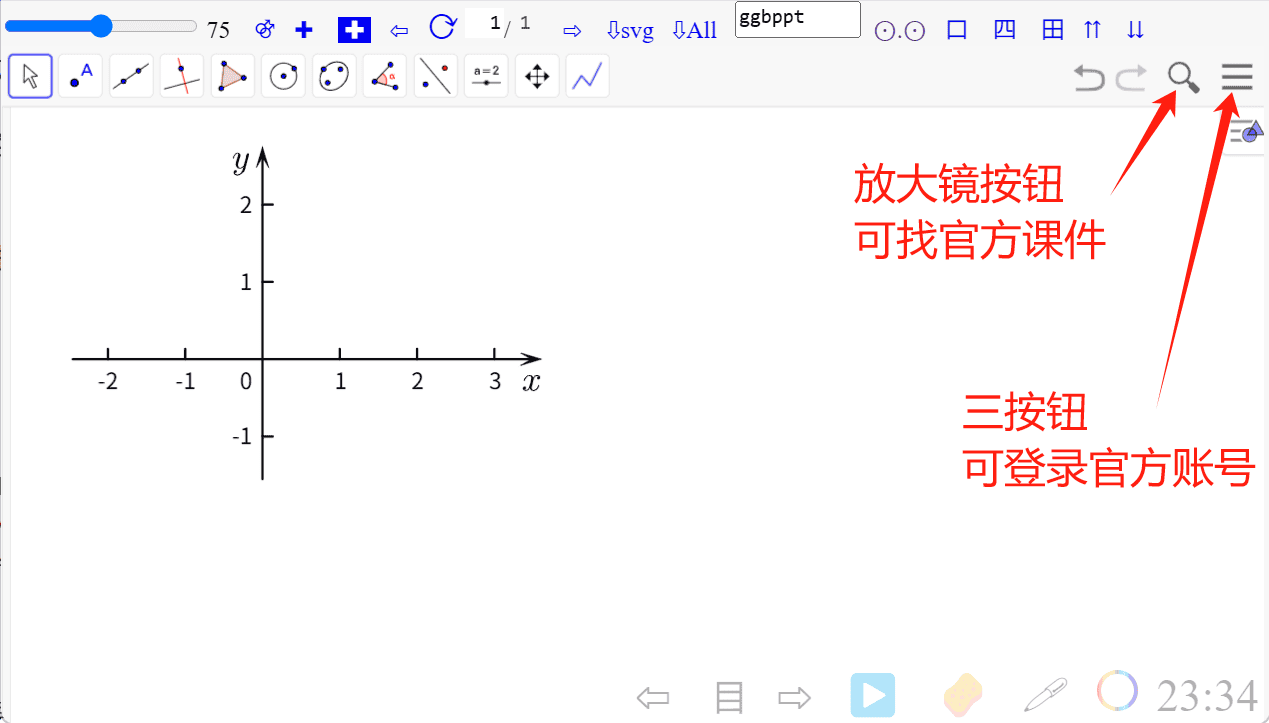
导入官方课件
- 方法一: 点击放大镜按钮, 找到一个想要的官方课件后, 点击课件就可导入
- 方法二: 把官方课件链接 https://www.geogebra.org/m/vjvvqxdw 修改为 https://www.geogebra.org/classic/vjvvqxdw, 进入页面然后组合快捷键crtl shift + B, 可自动复制长串字符, 粘贴到长框中, 最后点击按钮
⇊

1.6.6. 保存与导出文件
-
方法一: 打开离线包中的
启动.bat, 不要关闭黑色框, 就可以crtl s或✔保存文件 -
方法二: 先点击
✉定位, 再crtl s或✔保存文件 -
⇩All按钮可以一键导出当前html文件, 把该html文件分享给好友, Ta无需安装软件就可以打开多页课件
1.6.7. 分享多页课件
优势是, 分享给好友. Ta无需安装软件就可以打开多页课件
- 方法一: 点击右上角
三按钮, 登录官方账号, 再点分享按钮, 可得分享链接
- 方法二:
目按钮开启目录区域, 输入分享口令, 再点分享📤按钮会自动打开分享界面; 为了防止滥用, 分享口令需要进群申请; 需要注意的是这种方法得到的链接是公开的, 任何人都可以查看
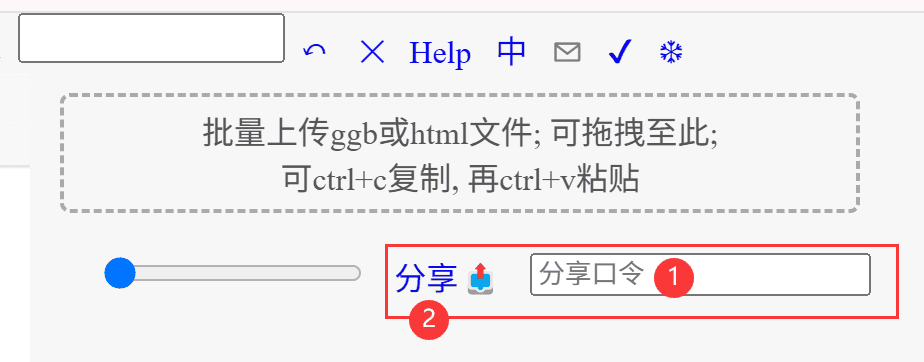
- 方法三:
⇩All按钮可以一键导出当前html文件, 然后把html文件发送给好友
1.7. ggb版本的更新
只需两步:
- 下载并解压官网最新网页离线包 https://download.geogebra.org/package/geogebra-math-apps-bundle
- 找到新版本
web3d文件夹, 然后替换多页版里的geogebra/5.0/web3d文件夹
2. GeoGebra必用操作
2.1. 链接转换
2.2. 常用快捷键与输入
| 快捷键 | 功能 |
|---|---|
| Ctrl Shift+ A | 显示或隐藏代数区 |
| Ctrl Shift+ C | 复制绘图区的图片 |
| Ctrl E | 显示或隐藏设置 |
| Alt + 右键框选 | 把框选对象加入到列表 |
| Alt + O | ∘ |
| Alt + P | π |
| Alt + I | 虚数 |
| Alt + S | 根号 |
| Alt + A | α |
| Alt + b,g,t,L | β, γ, θ, λ |
输入sqrt |
根号 |
| Shift + 6 | 上角标 |
| Shift + - | 下角标 |
2.3. 保存ggb文件
- 界面右上角
三字形状的图标--->Download as--->ggb
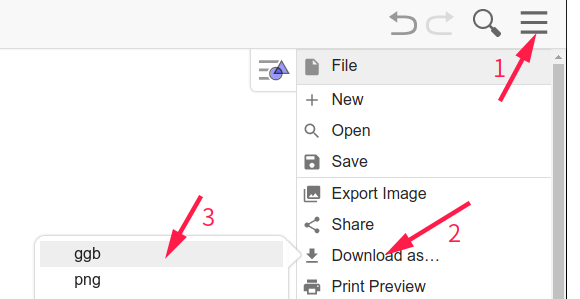
- 其实最简单的办法是点击页面 https://kz16.top/ggb 最上方的
⇩All按钮即可联网使用(文件可直接分享给好友), 保不保存ggb文件无所谓.
2.4. 下载官网ggb课件
-
最实用的办法是:
点击动态图, 按组合快捷键
Ctrl+Shift+B
可复制一长串ggbbase64代码, 然后按快捷接
Ctrl+V
把ggbbase64代码粘贴到 https://kz16.top/ggb 最上方的长条输入框中, 最后点击⇊按钮 -
其它办法:
例如找到了一个比较喜欢的官网例子
https://www.geogebra.org/m/jmskq7v9
只需要把链接改成
https://www.geogebra.org/classic/jmskq7v9
2.5. 导入图片
-
法1: 紧按鼠标左键, 直接把图片拖入到画图的界面中
-
法2: 点击最上边滑动条那个图标--->Image--->Choose File
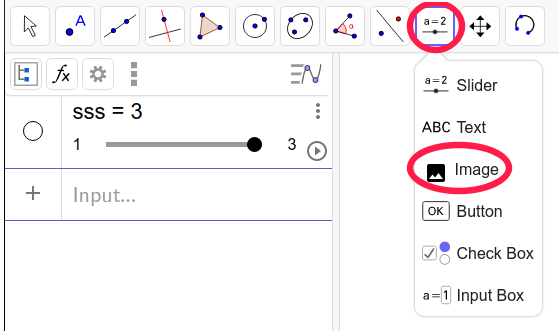
2.6. 提取ggb中被插入的图片
- 只需要把ggb文件用解压软件解压即可, 推荐用免费无广告的 https://7-zip.org/ 解压, 用解压软件解压.ggb文件一定有惊喜!
2.7. 矢量图的转换
经典5导出的图不好看, 并且经典5文本有锯齿
网页版或6, 导出来的svg, 真是所见所得, 而且看起来舒服
如果要得到其它格式的矢量图(例如eps, pdf等)怎么办呢?
用inkscape即可, 它也是非常优秀的画图软件, 用它转换图片格式非常轻松
https://inkscape.org/gallery/item/53697/inkscape-1.4_2024-10-11_86a8ad7-x64.msi
3. GeoGebra必学技巧
3.1. 常用小技巧
-
绘图的过程中, 点了绘图小图标工具后一定要记得点击左上角的剪头, 确保是移动状态
-
鼠标右键可设置属性, 或者框选多个对象
-
Shift或者Ctrl可以一次性选择多个对象
-
尽量用代码画图, 推荐代码用markdown编辑器保存起来, 参考 https://kz16.top/md/ , 在线markdown, 推荐使用 https://code.kz16.top
-
对不熟悉的指令, 可以用必应或者谷歌搜索, 搜索的词条为
geogebra 指令名, 例如geogebra zip, 一般第一条就会得到指令解释
3.2. 循环与求和
3.2.1. 序列循环zip
-
推荐用
zip, 完全没必要用sequence例如得到列表
{1,4,9,16,25,36}可以这样写zip(k^2,k,1..6)
3.2.2. 迭代Iteration
-
IterationList
iterationList(p*10+1, p, {1}, 2)
结果为{1, 11, 111}斐波那契数列
iterationList(b+a, a, b, {1, 1}, 5)
结果为{1,1,2,3,5,8} -
Iteration
iteration(p*10+1, p, {1}, 2)
结果为{111}
3.2.3. 序列求和Sum
- 求和要注意大写, 求列表
{1,4,9,16,25,36}的和
Sum(k^2,k,1,6)
要注意:
zip括号中的1..6是用两点隔开的
Sum括号中的1,6是用逗号隔开的
3.3. 判断
例如绘制分段函数
f(x)=if(x<0,-1,x<1,x,1)
此外可能偶尔用到keepif以及countif
如果想绘制椭圆的一部分图像, 推荐用参数方程作为判断, 而不是对隐函数做判断, 因为GeoGebra的隐函数功能很弱, 例如绘制椭圆的第一象限:
curve((2cos(t), sin(t)),t,0,pi/2)
如果用隐函数可以这样:
x^2/(x>=0) + y^2/(y>=0) = 1
3.4. 列表
列表从某种意义上可以被认为是集合或多维向量, 列表中可以有数也可以有其它对象, 例如点, 线, 多边形等, 同数学中的集合一样, 用{}把元素括起来. 常用的指令及相关技巧有:
-
1..4得到结果{1,2,3,4} -
合并
join, 展平flatten可分别看例子
join({1},{2,{3}})得到{1,2,{3}}
flatten({{1},{2,{3}}})得到{1,2,3} -
a(1)或element(a, 1)表示列表a的第一个元素,a(-1)表示列表a的最后一个元素,element(a, -1)会报错 -
take(a,2,4)表示取列表a的第2,3,4号索引, 例如
take(1..6,2,4)得到2,3,4 -
Union(a,b)表示a,b的并,Intersection(a,b)表示a,b的交 -
属于符号
∈完全和数学一致 -
对列表循环, 通常用
zip函数, 例如得到列表a={1,3,1,4}的平方, 可以这样
zip(k^2,k,a)也可以直接a^2结果都是{1,9,1,6} -
同时对多个列表循环, 例如计算2个列表的和
a={1,2,3} b={4,5,6} zip(ak+bk,ak,a,bk,b)
上面最后一步当然也可以直接写成
a+b
其它一些操作, 列表可以当成某个特殊的数, 例如
-
{1,2}*3结果为{3,6} -
{1,2}+{3,4}结果为{4,6} -
ln({1,e,e^2})结果为{0,1,2} -
... 其余的可自己去尝试
一个非常使用的框选多个点转变为列表的操作为:
紧按Alt+ 鼠标右键 框选点最后回车即可.
列表的数据导出来,可先导出为html文件,然后打开html文件,即可复制列表中的数据.
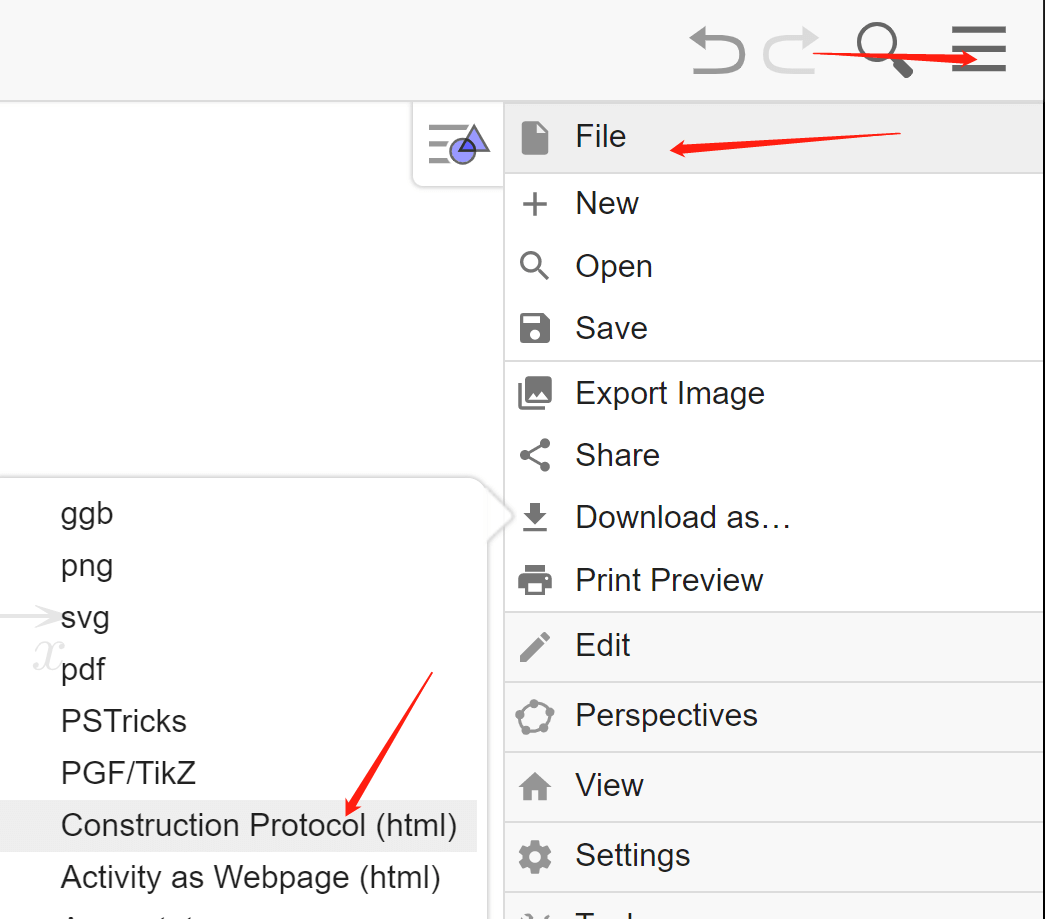
3.5. 向量与点
向量和点在某种意义下可以认为是同一个类对象, 都可做向量的基本加减和数乘运算, 稍微有点区别的是, 向量会有个箭头, 并且一般默认用小写字母表示向量, 大写字母表示点
-
若
A=(1,2), 则x(A)=1,y(A)=2 -
若
A=(1,2),B=(3,0), 则它们的中点为(A+B)/2 -
用分号隔开则表示极坐标, 例如
B=(1;pi/3)
3.6. 复数
复数的基本表示方法和数学没什么区别, 例如
Z=1+3i
它的一个很大的作用是, 把某个对象乘以复数, 等于是做旋转和伸缩变换, 例如, 若A=(1,2), 则i*A或A*i结果为-2+i
这样使得代码变得简洁, 当然可能不利于新手阅读代码
3.7. 插入特殊的标记对象
例如插入一个花括号, 把两个自由的点括起来
- 制作透明花括号的svg矢量图片
t=text("\overbrace{\qquad\qquad}",(0,0),true,true)- 右键框选花括号图片, 并输入下面代码, 回车
ExportImage("filename","image.svg","type","svg")
- 导入上一步的花括号图片
image.svg, 默认导入的图片为辅助对象, 第一个图名字为pic1 - 接下来就是控制图片的大小, 任意绘制2个点
A,B, 并且
C=A+i (B-A)/abs(A-B)*aaa*4,
然后右键设置图片的三个角点位置别为A,B,C. 这样调整A,B括号会自适应改变 - 如果要绘制多个花括号, 就复制图片
CopyFreeObject(pic1)或者再上传一次图片, 然后重复操作
如果使用频率高, 可以把上面的步骤做成工具
3.8. 参数方程
总得来说分成三类: 圆弧, 折线和一般曲线
3.8.1. 圆弧的参数方程
求圆弧ABC, 的参数方程
A=(0,0) B=(1,0) C=(0,1) Q=center(circle(A,B,C)) r=abs(Q-A) t1=angle(A-Q) d=cross(A-C,B-C) t3=if(d>0,angle(A,Q,C),angle(C,Q,A)) c=curve(Q+(r;t1+t3*t*sgn(d)),t,0,1)
这里需要设置角度的范围为0-360, 因此推荐用本文提供的模板, 无需自行设置, 并且做成了工具, 工具名为arct
https://kz16.top/ggb
输入的是圆弧上的三个点, 例如arct(A,B,C)
3.8.2. 折线参数方程
Lp = {(0,1),(2,1),(1,3)} n = length(Lp)-1 f(x)=Function(join({0,n},x(Lp))) h(x)=Function(join({0,n},y(Lp))) a = curve(f(t*n),h(t*n),t,0,1)
对于一般线段AB的参数方程可以为
curve(A(1-t)+B*t,t,0,1)
在模板 https://kz16.top/ggb 中
工具polyt可以得到归一化参数方程, 也就是参数范围为[0,1], 工具polys得到弧长参数. 两个工具的输入参数都是点列, 例如 polyt({(0,1),(2,1),(1,3)})
折线参数方程数学理论可参考:
https://kz16.top/geogebra/polyarc.html
3.8.3. 一般曲线参数方程
pt = {(0,1),(2,1),(1,3)} a = spline(pt)
一般的参数方程, 推荐用样条插值, 多项式拟合可以选择FitPoly, 或者直接自行选择基函数再用fit函数拟合
3.9. 区域涂色
本质上是一个确定区域的数学题, 因此主要可以有这么几种方法
-
不等式法 : 只需知道
∧表示交,∨表示并,¬表示非, 或者分别用符号&&,||,! -
多边形 : 直接绘制多边形即可
-
参数方程 : 如果曲线首尾没有连接, 默认会用直线连上
这里主要讲万能的参数方程法处理对于一般的带有曲边和直边的区域涂色
给定一个区域, 和区域边界上任意的几个点A,B,C,D,E,F,G, 满足
ABC是曲线段
CD是线段
DEF是曲线段
FGA是线段
则该区域的涂色可以用如下GeoGebra代码绘制:
a = spline({A,B,C}) b = curve(C(1-t)+D*t,t,0,1) c = spline({D,E,F}) d = curve(F(1-t)+G*t,t,0,1) f = curve(if(t<1,a(t),t<2,b(t-1),t<3,c(t-2),d(t-3)),t,0,4) SetDynamicColor(f,0,0,1,0.3)
上面的方法用到了样条插值, 逼近效果是很不错的, 通常情况下可以处理几乎所有的区域涂色, 对于圆弧段曲线, 可以自行写出相应的参数方程. 相关参数方程的求法可回顾之前介绍的参数方程
参数方程着色稍微麻烦的地方就是合并参数方程
例如: 合并2个归一化的参数方程a与b可以表示为
Curve(if(t<0.5,a(2*t),b(2*t-1)),t,0,1)
重复下去, 可以把多个参数方程合并为一个
3.10. 模糊的png数学图转svg矢量图
实现这一步需要用到前面的经验和技巧
-
紧按鼠标左键, 把png图片拖到绘图区
-
在png图上临摹点, 如果是曲线就多加几个点, 对于折线或线段就绘制折点和端点.
-
用前面提供的参数方程的办法, 把线条用参数方程写出来
-
修改样式: 线条的粗细, 样式, 颜色等, 区域涂色, 适当注意下图层等, 隐藏不必要的点或标签. 这一步可以通过鼠标右边点击对象, 设置对象的属性或样式
-
如果要用LaTex公式标签, 记得选
serif和LaTex formula
LaTex相关常用符号, 可参考 https://kz16.top/latex/symbol/
4. 动态交互
有了前面的知识, 应该可以绘制绝大部分的静态图
对于动态交互图,
用得最多的是滑条Slider 其次是复选框和按钮(其实多数情况下复选框比按钮实用, 甚至可完全按钮). 因此只需知道滑条和复选框的使用方法
4.1. 滑动条
创建滑动条
k=Slider(0,1,0.01)
没必要手动点, 直接输入代码就好, 这里有3个参数, 前两个是范围, 最后一个是增量, 不必担心记不住Slider这个单词, 输入前面两个单词就会有提示的, 而且多输入几次就记住了. 不推荐中文名字, 因为切换输入法太慢了
有了滑条可以绘制含参函数, 例如
f(x) = k*x^2
也可以做动点, 例如, 用滑条控制点做圆周运动
k=Slider(0,2pi,0.01) A=(1;k)
也可以控制三角形做旋转或平移运动
k=Slider(0,2pi,0.01) t1 = {polygon((0,0),(1,0),(0,1))} rotate(t1, k) translate(t1, (k,0))
上面的代码, 把polygon((0,0),(1,0),(0,1))用{}括起来是为了把它变成列表, 这样就不会出现额外的边对象
4.1.1. 动态轨迹
例如绘制下面的动态交互曲线
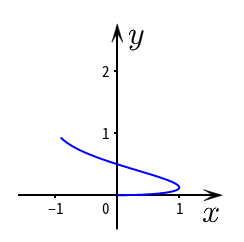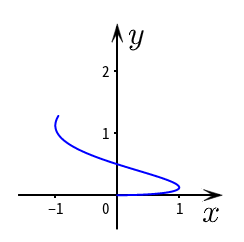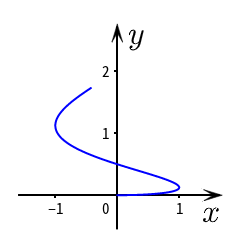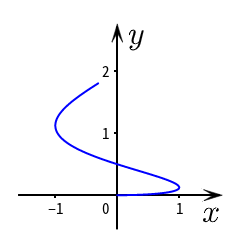
a = slider(0,1,0.01) b=Curve((sin(2π*t),2t^(2)),t,0,a)
或者用轨迹法(这种方案虽然麻烦, 但是比较具有一般性)
a = slider(0,1,0.01) f=segment((0,0),(0,a)) A=point(f,1) t = y(A) H=(sin(2π*t),2t^(2)) c=locus(H,A)
4.1.2. 滑动条在指定位置自动停留
在实际做演示过程中, 需要滑条在指定位置停留, 然后点击按钮会启动. 例如滑条在0,1,e,pi,6位置上自动停留
Lp={0,1,e,pi,6} n=slider(0,length(Lp)-1,1) n=1 b=slider(Lp(n),Lp(n+1),0.01, 10 / abs(Lp(1 + n) - Lp(n))) ## 上面的参数10可用于设置滑条速度 ## b 的 slider-->Repeat 设置为: Increasing (Once) a=slider(Lp(1),Lp(-1),0.01) ## a 的 On Update 脚本为: SetValue(a,b) t=button("start") ### t的 On Click 脚本为: SetValue(n, If(n==length(Lp)-1, 0, n)) n = n+1 StartAnimation(b, true) StartAnimation(a, true)
嫌弃上面代码麻烦, 不妨直接看成果
https://www.geogebra.org/classic/xsymtz3s
缺陷是往返设置略微麻烦
4.2. 复选框
如何通过按钮实现停止和启动滑动条? 可用复选框轻松搞定
-
创建滑条
k=Slider(0,1,0.01) -
创建复选框
a=true -
右键点
a--->Setting--->Scripting--->On Update, 然后把代码StartAnimation(k,a)粘贴到界面On Update下面的框中, 并且叉掉刚打开的Setting(设置)框

-
点击复选框
a左边的矩形按钮, 就可以实现停止和启动滑动条
4.3. 一次性导入多行的代码
代码太多, 一行行输入着实麻烦, 一次性导入多行代码其实也很简单
-
创建复选框
a=true -
右键点
a--->Setting--->Scripting--->On Update, 然后把多行ggb代码粘贴到On Update下面的框中, 并且叉掉刚打开的Setting(设置)框 -
点击复选框
a左边的矩形按钮, 可直接执行多行ggb代码
其实第一步也可以创建一个点或按钮, 不一定非要复选框
4.4. 导出动态图以及PPT展示
可以选择用gif或mp4录屏软件, 其实它的作用主要用于网络交流
对于非正式演示, 可以直接拿出ggb展示, 如果是多个ggb文件, 直接用网页版多页模板 https://kz16.top/ggb 即可
如果是正式场合, 推荐导出多张svg矢量图帧, 实现动态变化, 那么这里涉及两个问题:
-
一是导出的图需要大小一样, 并且连续两张图的变化要比较平和, 也就是要确保该固定的得固定, 该变化的得变化.
-
二是导出多个图片帧怎么插入PPT中做成动态效果? 其实在PPT中很容易处理的, 一种小白很容易实现的办法是: 先插入第一张图片, 再复制粘贴多个当前页面, 最后挨个翻页, 右键点图, 把每个页面的图片替换成目标图
对于上面提到的第一个问题, 用网页版多页模板 https://kz16.top/ggb 就比较简单了, 只需每变动一步, 点击页面最上方的克隆⚣按钮, 然后就可以鼠标左键点边框外的空白处, 按上下方向键翻页, 预览效果, 最后通过点击⇩svg可以逐个页面快速导出svg矢量图
这种做PPT动态图的方法, 确实有点麻烦, 但是效果是真的好, 为了效果, 正式场合耗费时间也是值得的
5. 交流分享
做好了动态ggb图, 希望可以保存在云端, 然后通过链接分享给别人, 或者只是自己私密保存, 这个其实非常简单, 以本文的网页版多页模板为例
-
官网 https://www.geogebra.org/ 或国内镜像 https://www.ggb123.cn/ 注册账号
-
在页面 https://kz16.top/ggb 里登陆, 具体步骤是: 右上角
三字形状的图标--->Sign in
-
右上角
三字形状的图标--->Share, 弹出一个窗口, 可以选择 Shared(分享) 或者 Private(私密), 这个可以根据需求选择, 然后点 SAVE(保存), 会弹出一个对话框, 里面有一个链接, 可以复制这个链接, 然后分享给他人

当然也可以直接在页面 https://kz16.top/ggb 上, 点击⇩All, 会得到一个html文件, 然后可以把这个html文件分享给他人, 对方可以直接用浏览器打开
6. 提问与回答
提问: 为什么叫多页模板
回答: 既提供多页功能, 又设计了一个超实用的画图模板
提问 请问多页模板是不是只有网页版才可以用?离线版不能用?
回答: 既可以在线,也可以离线。在线的意义有两个,1.用户用得少,就不需要下载离线包. 2.方便分享,你只需要一个html文件分享给好友,好友不需要安装任何软件可打开你的交互ggb. 离线包绝对是业界良心,免费开源,离线包体积小,跨平台,免安装,免登陆,双向兼容官方。最关键的是无门槛下载。也不需要登陆就可以用,可绝对离线使用
额外回答: 如果一个画图软件,文档软件或者笔记软件等办公软件。它必须要登陆才能使用,不能完全离线使用。无论它有多好用,都有很多风险:
-
没网络无法用。
-
你有网,它的服务器崩溃也无法用。
-
它突然收费或涨价,你只能乖乖就范。
-
它不干了或跑路,你的心血全没了!
可以接受的联网登陆是: 多端云同步, 多人协作.
无论如何强制联网登陆需要谨慎
提问: 如果自己电脑上做好ggb插入到wps ppt的课件后, 发给别人, 别人可以打开吗?
回答: 别人可以打开. 新电脑可以不安装wps演示催化剂(本地安装wps演示催化剂的好处是可以替换和编辑ggb离线网页的地址). 如果是本地离线链接, 需要有ggb离线多页包, 并一键打开启动.bat脚本. 如果是在线https链接则在有网络状态下即可实用, 无需额外下载安装任何软件和插件
提问: html文件是不是一定要联网?
回答: 不是的, 如果把html文件放到离线包中, 可以不需要联网; 没有离线包的情况下, 则需要联网才能正常显示
提问: 会收集用户数据吗? 使用这个软件安全吗
回答: 多页模板不会收集用户的任何数据.
-
导出的多页html文件里面包含多个base64代码. html文件可通过文本编辑器打开查看, 或者直接用谷歌浏览器打开, 然后快捷键Ctrl U查看; base64代码包含了画图文件的所有信息, 手动把base64代码保存到
.ggb格式的文本文件中, 可以直接被GeoGebra桌面程序识别; base64代码也可以直接导入到多页模板里, 只需把长串的base64代码粘贴html页面的长框里, 然后点击⇊按钮. 也就是说多页html文件里的数据完全和官方GeoGebra数据互通. -
最新版本已经移除了
caddy.exe使得离线包体积非常小, 并且离线包中不存在exe文件.
提问: 需要付费和登陆吗?
回答: 不需要登陆也不需要付费, 包中所有软件都是开源的. 但是一定要注意GeoGebra软件是不能商用的. 因此该离线包的软件也是可免费但是不能商用. 本项目只是一个小小的公益项目.
提问: 我的机器是苹果电脑, 但是别人机器是win系统, 可以兼容吗
回答: ggb离线多页模板完全可以兼容不同的操作系统, 但是目前插入到wps ppt里不支持苹果系统
相关链接
- 必看非常实用------LaTex常用符号
- GeoGebra5.0官方下载: https://download.geogebra.org/installers/5.2/
- GeoGebra6.0官方下载https://download.geogebra.org/installers/6.0/
- GeoGebra网页在线https://geogebra.org/classic
- GeoGebra网页在线好用https://www.geogebra.org/classic/byjwhvmz
- 强烈推荐新版网页版多页模板: https://kz16.top/ggb
欢迎非商业转载,转载请指明来源
免责声明: 本开源项目, 源于2019年, 并逐步更新完善. 如果使用该项目引起的任何问题责任以及纠纷等, 本人概不负责.
补充说明: 本项目是基于下面开源项目(请自觉遵循相关协议)